前缀和
一维前缀和
主要思想:
- 求[l, r] l到r之间的和,比方说从第二个到五个数的总和可以表示为,前5个数的总和减去前一个数的总和:
s[l~r] = s[r] - s[l - 1],s为到第i个数的总和
- 默认s[0] = 0,来统一计算方式(节省了个if)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e6 + 10;
int n, m;
int a[N], s[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i)
s[i] = s[i - 1] + a[i];
while (m--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
|
二维前缀和
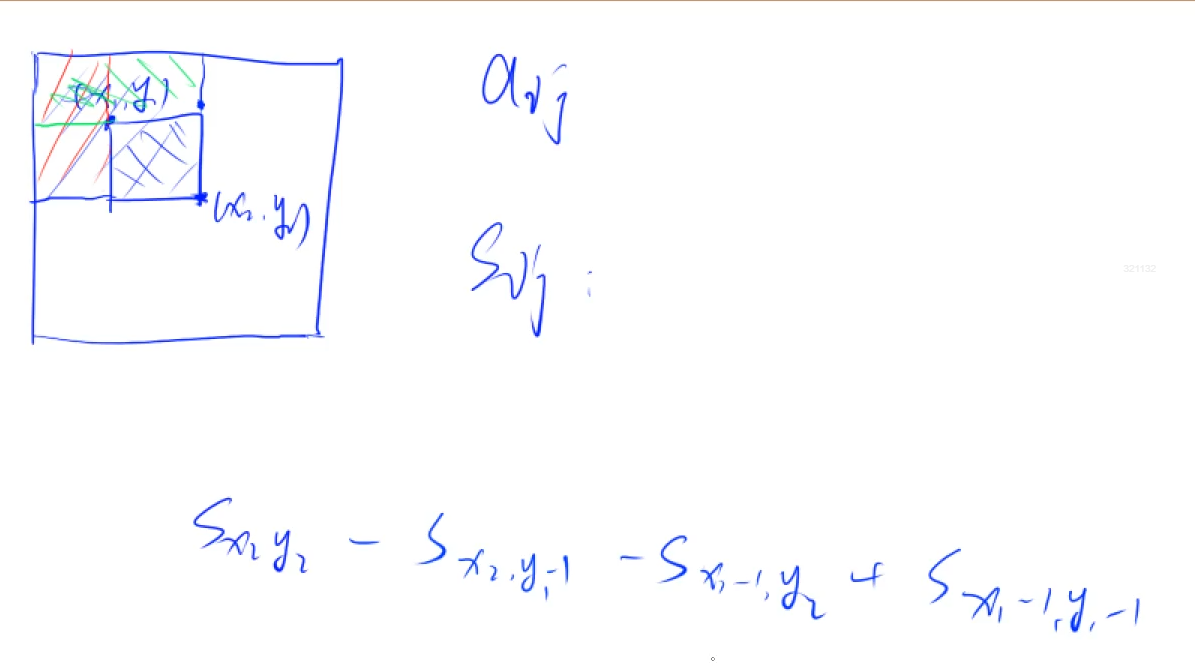
问题:求二维数组一块区域的前缀和
若要计算$s{x2_y2}$到$s{x1_y1}$, 就要减去俩个长方形的,然后加上重复减去的长方形的前缀和:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]);
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
while (q--)
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1-1]);
}
return 0;
}
|
差分
主要思想:
构造b1, b2, b3…, bn,使得a数组为b数组的前缀和:
1
2
3
4
| ai = b1 + b2 + ... + bi \\
b1 = a1 \\
b2 = a2 - a1 \\
bn = an - a_(n-1)
|
一维差分
用处:
这样可以通过求b数组的前缀和来得到a数组, 对于要求对于区间[r, l]中a+c,但其他a的值不变,想求改变之后a总共的和就只需要改变$bl$和$b{r+1}$的值 (O(1)),而不需要循环一边全部加上C(O(n))
1
2
| a_l -> b_l + c \\
a_{r+1} -> b_{r+1} - c (抵消之前加的c)
|
题目:
输入一个长度为n的整数序列,接下来输入m个操作,每个操作包含三个整数l, r, c,表示将列序中[l, r]之间的每个数都加上c。
输出进行完所有操作之后的序列
代码示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include <iostream>
using namespace std;
const int N = 100006;
int a[N], b[N];
int n, m;
void insert(int l, int r, int c)
{
b[l] += c;
b[r + 1] -= c;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
for (int i = 1; i <= n; ++i)
insert(i, i, a[i]);
while (m--)
{
int l, r, c;
scanf("%d%d%d", &l, &r, &c);
insert(l, r, c);
}
for (int i = 1; i <= n; ++i)
b[i] += b[i - 1];
for (int i = 1; i <= n; ++i)
printf("%d ", b[i]);
return 0;
}
|
二维差分
主要思想:
如下图,在二维数组中,仅让x_1, y_1到x_2, y_2的点之间的数加一个数C。这时可用差分来仅改变四个数的值来求一次和,而不用每次都遍历求和

题目:
第一行包含整数 n,m,q,接下来 n 行,每行包含 m 个整数,表示整数矩阵。接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
要求输出:共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
代码解答:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &a[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
insert(i, j, i, j, a[i][j]);
while (q -- )
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
puts("");
}
return 0;
}
|


